Цели урока:

Обучающая: обобщить и систематизировать знания, умения учащихся по теме «Элементы тригонометрии»; дать представление учащимся о важных веках истории развития математики.
Развивающая: развить познавательный интерес учащихся, память, воображение, мышление, внимание, сообразительность.
Воспитывающая: воспитание умения повышения активности, давать самооценку, чувствовать свои достижения, критически подходить к слабым сторонам.

Тип урока: Урок обобщения и систематизации знаний учащихся.

План урока:

1. Организационный момент.
2. Станция «Угадай тему урока»
3. Станция «Устная работа»
4. Станция «Вспомни»
5. Станция «Из истории»
6. Станция «Тест»
7. Станция «Итог урока»
8. Станция «Домашнее задание»

Ход урока:

1. Организационный момент.

(Сообщить цели урока).

2. Станция «Угадай тему урока».

Учащимся предлагается разгадать ребус.

Задание для первого варианта:

Вычислите:

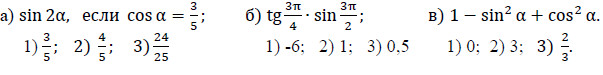
Ключ к ответу:

Задание для второго варианта.

Вычислить:

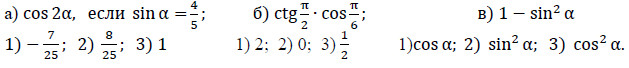
Ключ к ответу:

3. Станция «Устная работа»

1. Что называется углом в 1 радиан?
2. Что называется нечетной функцией?
3. Тригонометрическое тождество — это…
4. Что называется формулами сложения?
5. Чему равен синус разности двух углов?
6. Назовите формулу косинуса двойного угла.

4. Станция «Вспомни»

Преобразуйте тригонометрические выражения

5. Станция «Из истории»

Тригонометрия, как и вся научная дисциплина, возникла благодаря практической деятельности человека.

Основы тригонометрических знаний появились еще в древности.

Само слово «тригонометрия» греческого происхождения, в переводе на русский язык оно означает «измерение треугольников».

Древнегреческий ученый, выдающийся астроном Птолемей (II в.) разработал «тригонометрию хорд», которую изложил в своем главном труде «Альмагест». Птолемей вывел соотношения между хордами в круге, которые равносильны современным формулам синуса половинного и двойного углов, суммы и разности двух углов:

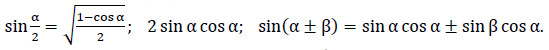
Важный шаг в развитии тригонометрии был сделан индийскими учеными, которые заменили хорды синусами.

Основополагающее значение в формировании тригонометрии как самостоятельной науки имели труды среднеазиатских ученых IX- XIII вв. Учение о тригонометрических неизменно строилась на геометрической основе. Общепринятые понятия тригонометрии, а так же обозначения и определения тригонометрических функций сформировались в процессе долгого исторического развития.

Лишь постепенно, благодаря введению новых понятий, а также в результате разработки и усовершенствования математической символики, тригонометрия приобрела современный вид, наиболее удобный для решения вычислительных задач. Окончательный вид она приобрела в XVIII в. в трудах Л. Эйлера.

6. Станция «Тест»

Задания на индивидуальных карточках:
(Работу учащиеся выполняют самостоятельно).

7. Станция «Итог урока»

При подведении итогов урока учащимся предлагается закончить предложения, написанные на доске:

— сегодня на уроке……….
— сегодня на уроке я узнал……..
— сегодня на уроке мое настроение……..
— сегодня на уроке я работал………

8. Станция «Домашнее задание»

Решить задачу: Что вы увидите, если посмотрите в наполненную водой кастрюлю под небольшим углом к горизонту? Вам покажется, что дно кастрюли приподнялось. Каков угол падения луча, если угол преломления вдвое меньше?